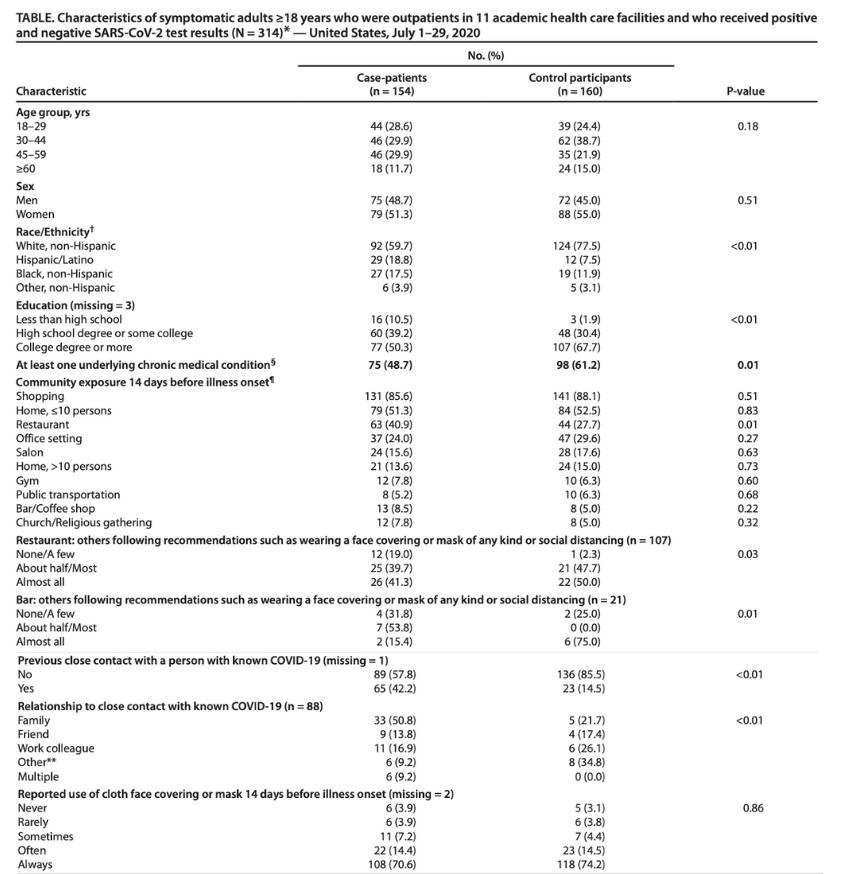
Reading tables is a core science skill that can seem a bit daunting at first, but let’s break this down. In the left-hand column are all the kinds of information the authors gathered about the study participants: age, sex, race, education, chronic medical conditions, and types of community exposure. The second and third columns show the number of people in the case-patient group and the control-participant group who have those characteristics, followed (in parentheses) by the percentage of the total that number represents.
You can ask your students questions to see whether they can interpret the table correctly. How many subjects over sixty years of age were in the study (42)? How many tested positive (18) and how many tested negative (24)? What percent of subjects had less than a high school education (12.4%)? What percentage of subjects had less than a high school education and tested positive (10.5%) and negative (1.9%)? When you’re sure your students are confident navigating their way around the table, you can turn to the last column: the p-value.
Some high school students may have learned some basic statistics and understand how p-values are calculated, but for the purposes of understanding this study, it’s really only important that they know this: the smaller the p-value, the more likely it is that the difference you see between the two groups is not due to chance. A p-value of 0.05 means that there is a 95% chance that the difference is real, not random. A p-value of 0.01 means that there’s only a 1% chance that the differences are due to chance.
Remember that in this case, the difference between the two groups is whether or not the subjects tested positive for coronavirus. Scanning down that right-hand column and looking for low p-values, what do you find? One thing that jumps out right away is that testing positive correlates very strongly with race and ethnicity. Hispanic/Latino and Black subjects are much more likely to test positive (p<0.01). This result is consistent with lots of evidence that Black and Latino Americans are less likely to have jobs that can be done at home and are more likely to live in multi-generational households, and therefore are more likely to be exposed to the virus. Education levels also are predictive of who will test positive; people with college degrees are more likely to be able to work at home and reduce their exposure—and sure enough, testing negative is correlated with higher education level at a p-value of <0.01.
I don’t need to say that these results do not mean that Black and Latino people, or people with less education, are innately more vulnerable to the virus, do I? I hope not. But it might be good to check in with your students and make sure they don’t come away with any misconceptions along those lines.
But now, finally, we get to the heart of the paper. Look down the p-value column next to the various community activities. What do you see? That’s right: a p-value of 0.01 for having been to a restaurant in the 14 days before testing. The next lowest p-value (0.22) shows up for having been to a bar or coffee shop. Lots of other activities, such as going shopping, or to a salon, don’t appear to increase the likelihood of testing positive for the virus.
So what does the experience of going to restaurants or bars have in common compared to those other activities? The authors suggest that the difference is that most of the other activities can be done while wearing a mask, reducing the risk of spread. But in a restaurant or a bar, you must remove your mask at least part of the time. This study suggests that these activities, therefore, are riskier than going shopping or even going to a gym.
Remember, way back in May 2020, we discussed how to decide what activities are riskiest and how to spend your “risk budget” wisely? Well, what this study tells you is that eating in restaurants seems to be riskier than shopping or going to a salon (assuming, of course, that you wear your mask and so does everyone else). You can adjust your risk budget accordingly.